TEMEL İSTATİSTİKSEL TAHMİN SÜREÇLERİ
Tedarik Zinciri Planlama Çözümleri kapsamında, talep planlama süreçlerinin detaylarını paylaşacağım blog serimizin ilkinde, tahmin süreçlerinde temel ve gelişmiş istatistiki tahminleme modellerinin işletmeye uygunluğunu belirlemek ve işletmeye uygun istatistiksel tahmin süreç akışının nasıl olduğunu anlatacağım.
1. İstatistiksel Tahmin Yöntemleri
Bir analist veya veri bilimcisi olarak, çeşitli tahmin sonuçları elde etmek için tahmin modellerinin oluşturulması ve düzenlenmesi gerekmektedir. Tahmin Algoritmaları, dinamik olarak değiştirilebilen ve kullanıcıya özgü tasarlanabilen süreçlerdir. SAP DP (Demand Planning) talep tahmin fonksiyonları sayesinde, uzun ve orta vadeli dönemler için talep tahmin algoritmaları oluşturulabilir ve değiştirilebilir.
Talep planlayıcısı olarak birden fazla ürün veya ürün grubu için her hafta ya da ayda bir tahmin çalıştırılabilir. Hatta her gün güncel geçmiş satış verisini kullanarak anlık olarak değişen talep dalgalanmalarına göre günlük tahmin çalışabilirsiniz. Tahmin hesaplama süreçleri ardından günlük raporlar kullanarak rakamları etkileşimli olarak inceleyebilir ve düzenleyebilirsiniz.
İstatistiksel Tahmin Süreç Adımları
Süreç 1:
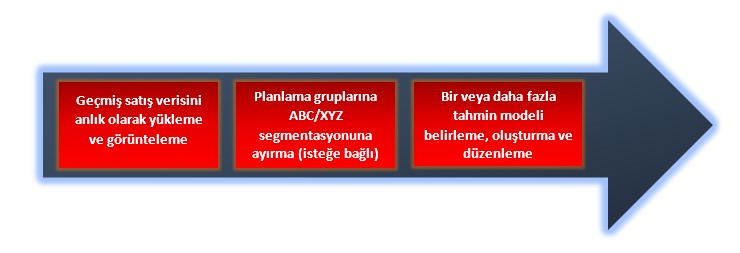
Süreç 2:
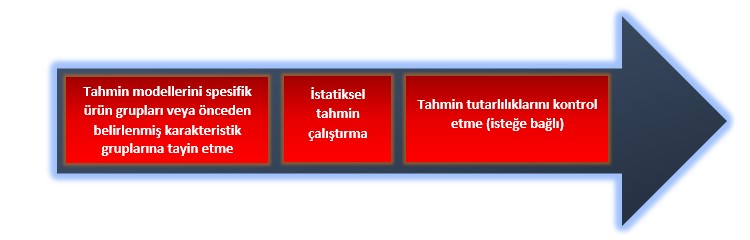
Bunlara ek olarak süreç içerisinde anlık alarm iletileri alınabilmektedir. Günlük raporlama arayüzleri oluşturulmaktadır.
İstatistiksel tahmin modelleri temel ve gelişmiş seçenekler olarak ikiye ayrılmaktadır. Bazı genel ayarların yanı sıra, bir tahmin modeli ön izleme, tahmin ve işlem sonrası algoritmalar içerebilir. Bu makalenin odaklandığı ana amaç mevcut istatistiki tahmin modellerini iş süreçlerimize uyarlayabilmektir.
2. Temel Tahmin Modelleri
Temel tahmin modellerini inceleyecek olursak;
- Basit Ortalama (Simple Average)
- Basit Hareketli Ortalama (Simple Moving Average)
- Basit Üstel Düzleştirme Yöntemi (Single Exponential Smoothing)
- Holt Üstel Düzleştirme Yöntemi (Double Exponential Smooting)
- Winters Üstel Düzleştirme Yöntemi (Triple Exponential Smoothing)
2.1 Basit Ortalama (Simple Avarage)
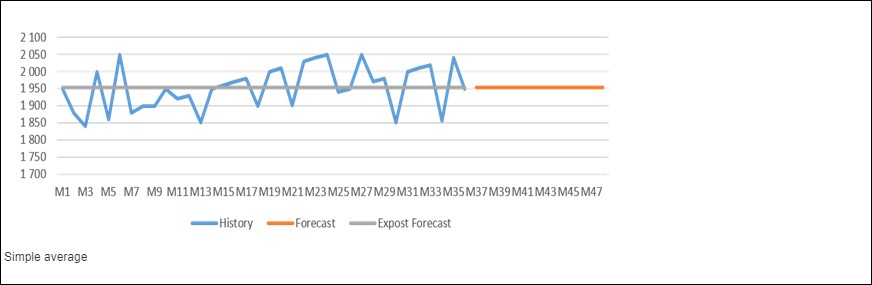Adından da anlaşılacağı gibi, bir değer kümesinin basit ortalaması, tüm değerlerin toplamının kümedeki değer sayısına bölünmesiyle belirlenmektedir.
Bu algoritma genellikle, oldukça istikrarlı satış sayılarına sahip ürünlere olan talebi tahmin etmek için kullanılır. Zaman ufkundaki tüm geçmiş verilerin ortalamasını hesaplar ve bunları geleceğe yönelik bir tahmin olarak kullanır. Ortaya çıkan tahmin, haftalık veya aylık geçmişe dayanan sabit bir sayıdır.
2.2 Basit Hareketli Ortalama (Simple Moving Average)
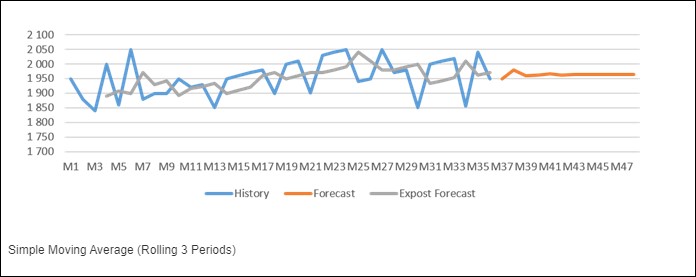
Basit Hareketli Ortalama, ağırlıksız bir hareketli ortalamadır.
Ağırlıksız: Veri kümesindeki her periyodun eşit önemde olduğu ve eşit derecede ağırlıklandırıldığı anlamına gelir.
Her dönem sona erdiğinde, en eski veri noktası çıkar ve en yenisi başa eklenir. Bu algoritma genellikle, oldukça istikrarlı satış sayılarına sahip ürünler için bir satış tahmini oluşturmak için kullanılır.
Üstel Düzleştirme Yöntemi Nedir?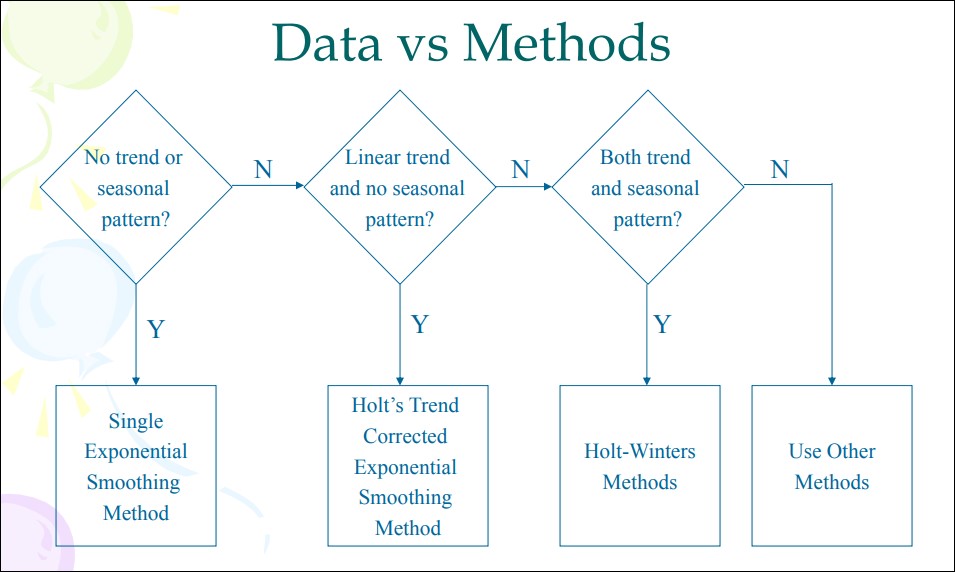
- Üstel düzleştirme yöntemi, verilerdeki son değişim ve sıçramaları dikkate alarak tahminlerin ya da öngörülerin devamlı güncelleştirildiği bir yöntemdir. Bu kapsamda zaman serisi verilerinin üstel düzgünleştirilmesi, en yeni ve en eski gözlemler için katlanarak azalan ağırlıklar tayin edilmesidir. Başka bir deyişle, veri büyüdükçe, veriye daha az öncelik (“ağırlık”) verilmektedir. Daha yeni veriler daha alakalı olarak görülür ve daha fazla ağırlık verilir. Yumuşatma parametreleri (yumuşatma sabitleri) – genellikle α ile gösterilir – gözlemlerin ağırlıklarını belirler.
- Zaman içinde değişen parametrelere sahip olan ve bir regresyon doğrusu ya da eğrisine dönme eğilimi olmadığından tek bir regresyon doğrusu ya da eğrisiyle açıklanamayan yani kısaca stokastik trende sahip olan serilerin analizi üzerinde durulacaktır.
- Üstel düzleştirme yöntemi hem deterministik hem de stokastik trende sahip olan tüm serilere uygulanabilmektedir.
- Üstel düzeltme genellikle kısa vadeli tahminler yapmak için kullanılır, çünkü bu tekniği kullanan daha uzun vadeli tahminler oldukça güvenilir olmayabilir.
Bu bölüme kadar anlatılan yöntemler, zaman içinde değişmeyen parametre varsayımına uygun serilerin tahminlerinde kullanılmaktaydı. Bu tür seriler deterministik trende sahip serilerdi.
2.3 Basit Üstel Düzleştirme Yöntemi (Single Exponential Smoothing)
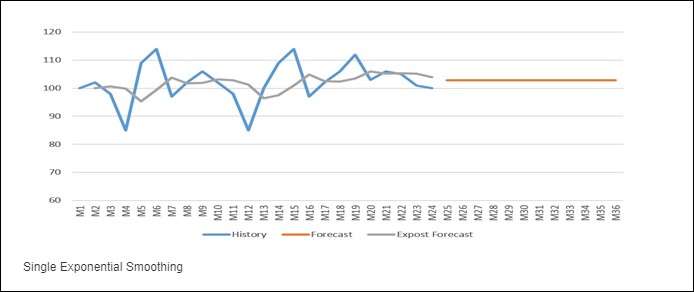
Bu yöntem trende ve mevsimsel dalgalanmaya sahip olmayan sadece bir ortalama düzey etrafında hareket eden serilerin analizinde uygulanmaktadır.
2.4 Holt Üstel Düzleştirme Yöntemi (Double Exponential Smoothing)
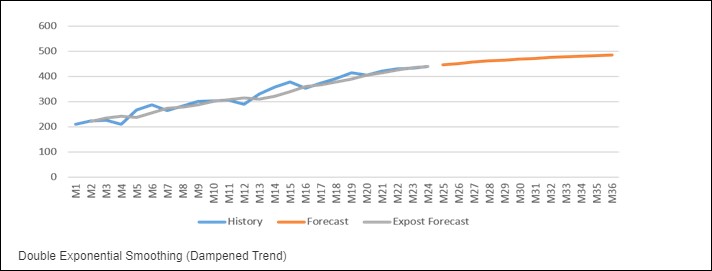
Holt metodu, zaman serilerinin, doğrusal trend ile izlenmesi için tasarlanmış bir yöntemdir. Trende sahip mevsimsel dalgalanması olmayan serilerin tahmin işleminde Holt Üstel Düzleştirme Yöntemi kullanılmaktadır. Bu algoritma genellikle verilerde bir eğilim gözlemlendiğinde yani büyüme veya düşüş aşamasında ürünler için bir tahmin oluşturmak için kullanılır.
2.5 Winters Üstel Düzleştirme Yöntemi (Triple Exponential Smoothing)
Bu algoritma, hem trend hem de mevsimsellik içeren bir zaman serisini modellemek için kullanılabilir. Öngörülen eğilimin uzun bir süre devam etmeyeceğini varsayarsak, eğilim azaltmayı kullanabiliriz. Bu durumda tahmin edilen eğilim tahminlerden aşamalı olarak kaldırılır. Bu yöntem önce serinin ortalama düzeyine, eğimine ve sonra mevsimsel bileşenine uygulanmaktadır.
Mevsimsellik, bir yıl veya daha kısa bir süre içinde ortalama talepten tekrarlayan ve öngörülebilir mevsimsel sapmalar anlamına gelmektedir. Veri kümenizdeki mevsimsellik niteliğini tanımlamak için aşağıdaki modellerden birini seçebilirsiniz.
Toplamsal Model
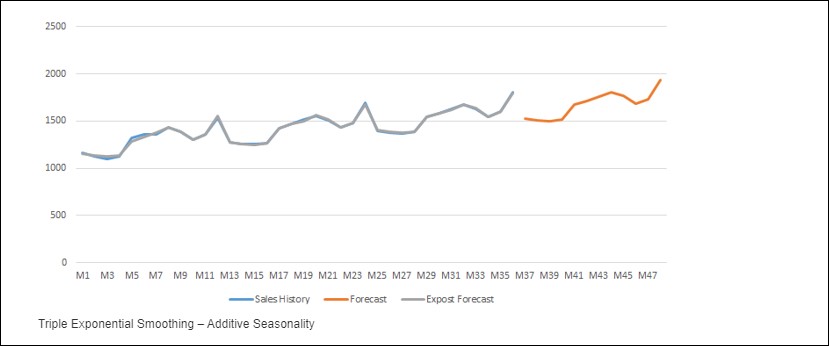
Veriler trend’den bağımsız ve mevsimsel hareketlerin büyüklüğü zaman içinde sabit varsayılır.
Çarpımsal Model
Mevsimsel hareketlerin trende bağlı olarak değiştiği ve trendin bir çarpanı olduğu varsayılmaktadır. Genellikle çarpımsal model tercih edilmektedir.
Sonuç olarak; kullanıcılar analiz etmek istedikleri veriler için uygun tahmin algoritmasını seçtiklerinde, net yön ve karar desteği sağlayacak raporlar ve veriler üretebilir ve paylaşabilirler. Doğru sonuçları elde etmek için, kullanıcının desene ve temel verilere dayanarak doğru tahmin algoritmasını seçmesi zorunludur.
Gelişmiş tahmin modellerinin ana hatlarına değineceğim sonraki blog yazımda görüşmek üzere.
Oğuz Çiçek
SAP APO Uygulama Danışmanı
